

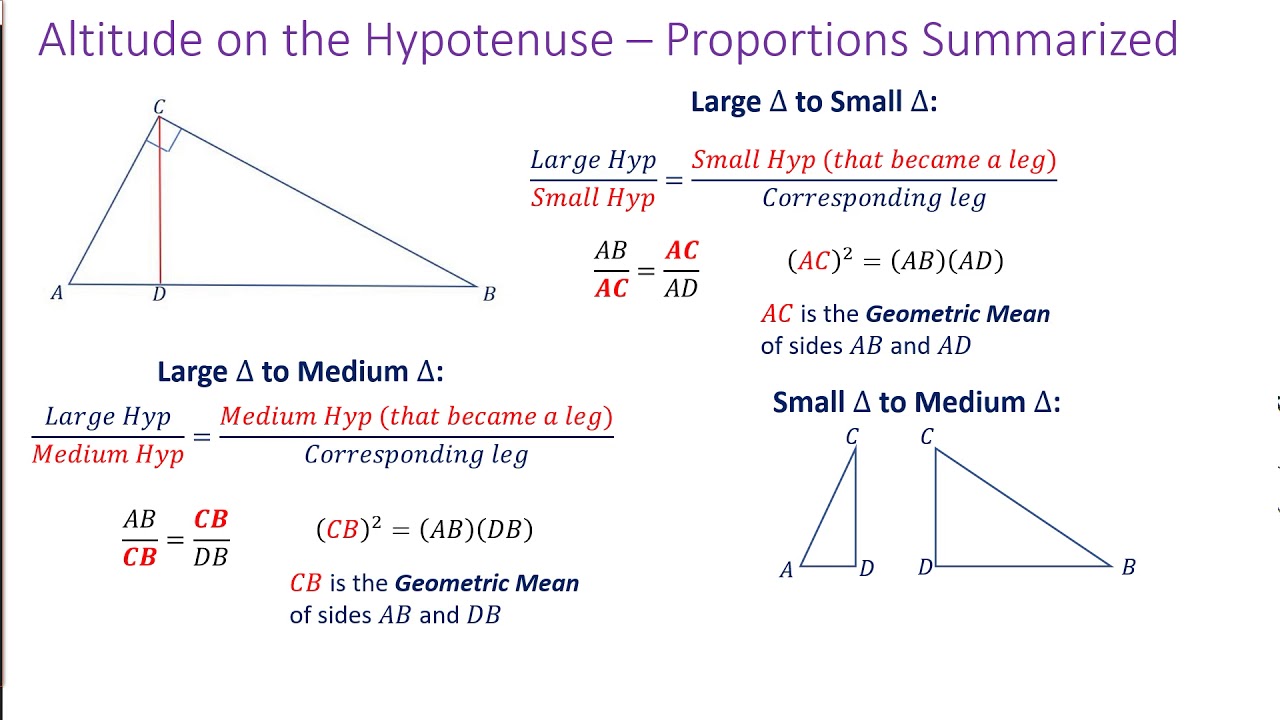
This proportion can now be stated as a theorem. PYTHAGOREAN THEOREM: DIAGONAL OF A BOX : DISTANCE IN CARTESIAN COORDINATE: The Pythagorean Theorem provides an easy way to compute the straight line distance between. RIGHT TRIANGLE: ALTITUDE, INRADII, INCENTER, AREAS. Math Education, High School, College, Elearning. so at 5,000 ft our standard temperature is 15C 10C 5C. The altitudes of a triangle are the Cevians AiHi that are perpendicular to the legs AjAk opposite Ai. Now, it’s important to note that we are at 5,000 ft above sea level here, so standard temperature is adjusted for altitude. Theorem 63: If an altitude is drawn to the hypotenuse of a right triangle, then each leg is the geometric mean between the hypotenuse and its touching segment on the hypotenuse. College Geometry Formulas, Pythagorean Theorem and Right Triangle Formulas. We have all that we need to calculate density altitude. These two proportions can now be stated as a theorem. This produces three proportions involving geometric means. Altitude of a cone, altitude of a cylinder, altitude of a parallelogram, altitude of a prism, altitude of a pyramid, altitude of a trapezoid, altitude of a triangle. Note that AB and BC are legs of the original right triangle AC is the hypotenuse in the original right triangle BD is the altitude drawn to the hypotenuse AD is the segment on the hypotenuse touching leg AB and DC is the segment on the hypotenuse touching leg BC.īecause the triangles are similar to one another, ratios of all pairs of corresponding sides are equal. The shortest distance between the base of a geometric figure and its top, whether that top is an opposite vertex, an apex, or another base. They have been drawn in such a way that corresponding parts are easily recognized.įigure 2 Three similar right triangles from Figure (not drawn to scale). Theorem 62: The altitude drawn to the hypotenuse of a right triangle creates two similar right triangles, each similar to the original right triangle and similar to each other.įigure 2 shows the three right triangles created in Figure . If we know the three sides ( a, b, and c. Every triangle has three altitudes (h a, h b and h c ), each one associated with one of its three sides. It can also be understood as the distance from one side to the opposite vertex. The following theorem can now be easily shown using the AA Similarity Postulate. The altitude of a triangle, or height, is a line from a vertex to the opposite side, that is perpendicular to that side. In Figure 1, right triangle ABC has altitude BD drawn to the hypotenuse AC.įigure 1 An altitude drawn to the hypotenuse of a right triangle. Summary of Coordinate Geometry Formulas.
Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.In slope intercept form equation of a line y mx + b, using the slope of AD and point A, find the y-intercept b. Classifying Triangles by Sides or Angles Altitude AD is passing through the point A.Further, we can also see below the different altitudes of triangle formulas for different triangles. Here the altitude is represented by the alphabet h. Lines: Intersecting, Perpendicular, Parallel The altitude of a triangle formula can be expressed as follows.The above example shows how problematic floating-point arithmetic can be. Other calculators may give some other inaccurate answer, depending on how they store values internally.
#ALTITUDE GEOMETRY FORMULA PLUS#
This is a problem because \(a=1000000 \), and so we would get \(s-a=0 \), causing Heron's formula to give us an area of \(0 \) for the triangle! And this is indeed the incorrect answer that the TI-83 Plus returns. the TI-83 Plus) will give a rounded down value of \(1000000 \). When we then divide that rounded value for \(a+b+c \) by \(2 \) to get \(s \), some calculators (e.g. Most calculators can store \(12\)-\(14 \) digits internally (even if they display less), and hence may round off that value of \(a+b+c \) to \(2000000 \).


 0 kommentar(er)
0 kommentar(er)
